If you toss a ball up gently, it may rise two meters in the air before falling back. If you throw a ball upwards as hard as you can, it might rise to a height of twenty meters. How fast must a ball be thrown in order to reach an altitude of one hundred meters? One thousand meters? One million meters? Is it possible to throw a ball up so fast that it never comes back down again?

If we throw a ball sufficiently fast, it will break free from the effects of the Earth’s gravity. The speed needed to escape out to infinity is called the Escape Velocity (Ve) and is calculated by equating Kinetic Energy with Potential Energy. On the other hand, the speed needed to go into a stable orbit (Vo) is calculated by balancing Centripetal Force with Gravitational Force. For a Low Earth Orbit, Ve is about 1.4 times Vo.

It is important to appreciate, Ve does not depend on the launch angle, but does depend on the initial starting altitude – oftentimes the height at which fuel burn ends.

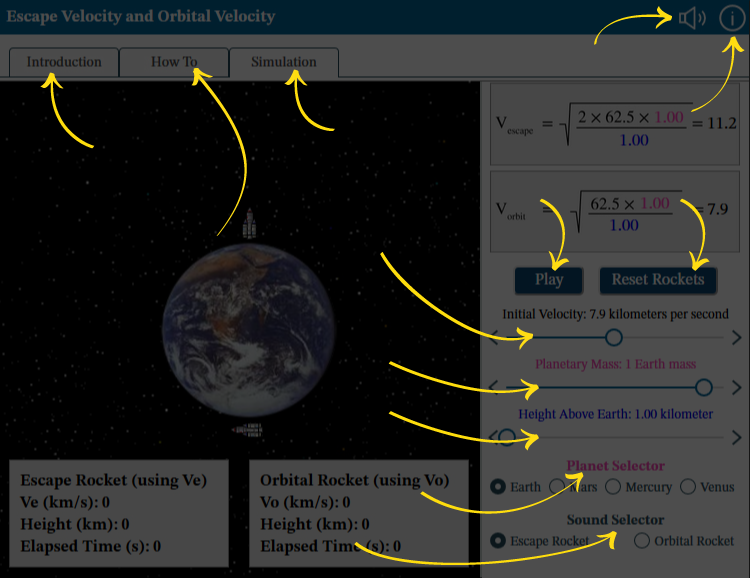
In the Interactive, we show two rockets, the one travelling vertically demonstrates the effect of Ve, while the horizontal rocket shows the effects of speed needed to enter orbit, Vo. In the interactive, we ignore air resistance effects and rocket fuel burn, i.e. we assume the rockets initial velocities are the result of fuel burn.

Your goal is to explore what it takes to keep a rocket in orbit around a planet (orbital rocket, launching horizontally) or to escape the planet’s gravitational pull completely (escape rocket, launching vertically). Find out what happens when you adjust both rockets’ initial velocity and height above the planet, which planet they launch above, and that planet’s mass.

The formulas region displays the equations for achieving escape velocity and orbital velocity based on the settings you have chosen.

Send the rockets on their way with the Play button. Pause the simulation at any time to find out both rockets’ current velocities, heights, and the elapsed time. The simulation does not end until you use the reset button. Reset returns the rockets to their starting positions but leaves the controls unchanged.

Choose to keep the sound off or listen to the path of either the escape or orbital rockets. If the sound is on, the tone will change to follow your chosen rocket’s trajectory. The higher-pitched the tone, the farther the rocket from the planet, the lower the pitch, the closer the rocket. The speed of the beeps indicates the velocity. Listen for the escape rocket slowing down before it falls back again and crashes. Listen for the changing distances of the orbital rocket’s orbit; a distinct tone will indicate a complete orbit.

Notes: Because the mass and radius are expressed in terms of the Earth's mass and radius, and the escape velocity is given in kilometers per second, the gravitational constant "G" has a value quite different from that shown in your textbook (in which the units are kilograms, meters, and meters per second, respectively). In addition, the Orbital Velocity calculation shown is for a perfectly symmetrical orbit; stable orbits can be achieved at other velocities.